Success - Smiley-CTF 2025 Write-up | My CTF Write-up Collection

Success - Smiley-CTF 2025 Write-up

Banner

Challenge: Success Category: Reverse Engineering Points: 50

Introduction

For this challenge, “Success,” we were given a Haskell source file (success.hs). The goal seemed pretty clear: figure out the correct input string that the program would accept as the flag. Looking at the source code, I saw a huge chain of checks that the input had to pass. It became obvious pretty quickly that trying to solve this by hand would be next to impossible, which suggested that I’d need to script a solution, probably using a constraint solver.

Step 1: Analyzing the (`success.hs`) File

The Haskell file is a simple program that you run from the command line with one argument. All the important logic is inside a function called checkFlag. Here’s what I gathered from reading it:

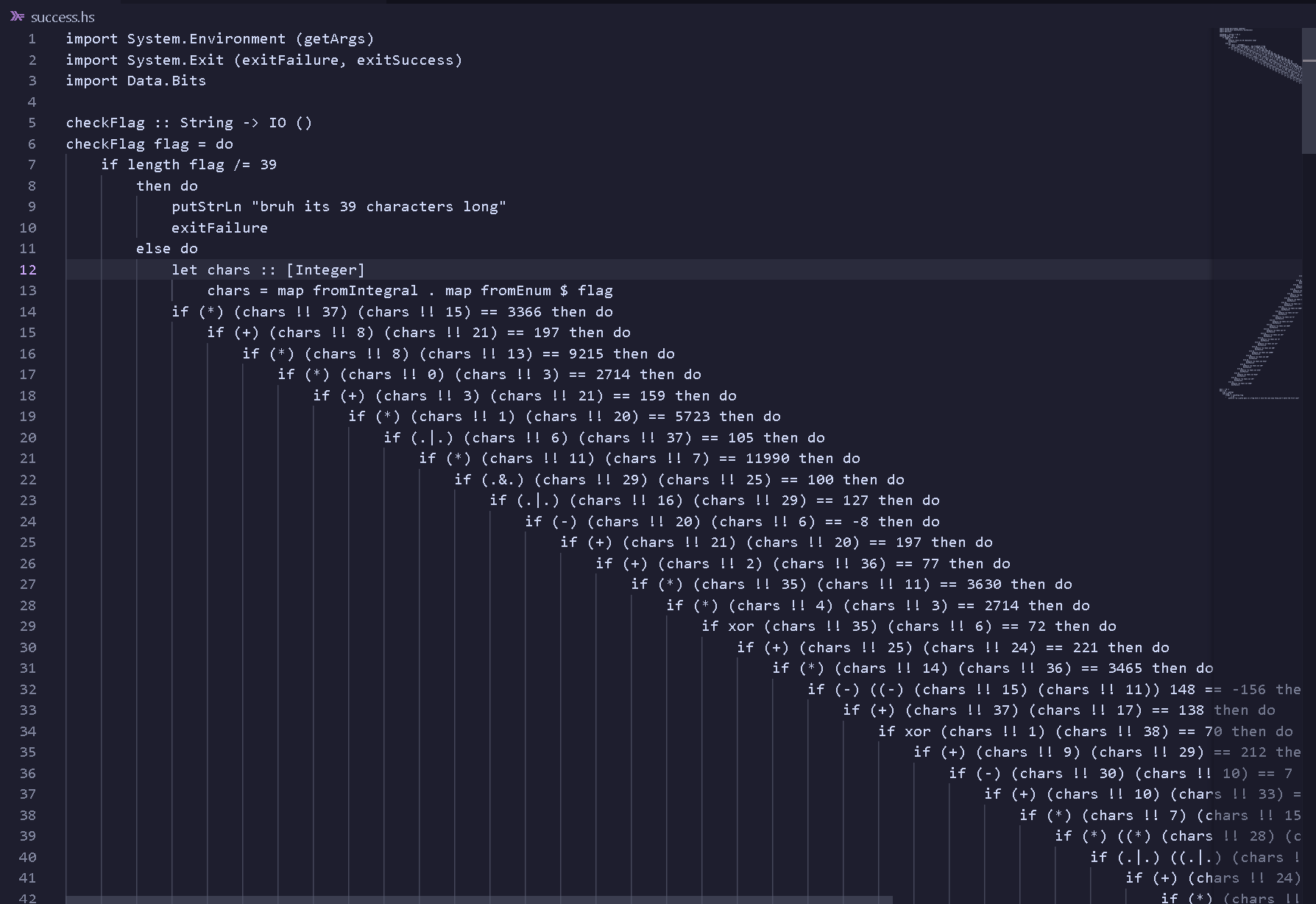
checkflag

Length Check: First off, it checks that the input flag is exactly 39 characters long.
To ASCII: Then, it takes all the characters from the input and turns them into a list of their ASCII values. It calls this list chars.
The Gauntlet of Checks: This is where it gets tricky. The code has a massive, nested if-then-else block with 57 different checks. To get the success message, the input has to satisfy every single one of these equations in order.
Success or Fail: If the input passes all 57 checks, we get a success message. But if even one check fails, it prints an error and stops.

All these checks are basically a big system of equations. For instance, I saw lines like:

(*) (chars !! 37) (chars !! 15) == 3366 (This looked like multiplication)
(.|.) (chars !! 6) (chars !! 37) == 105 (I figured this was a bitwise OR)
xor (chars !! 35) (chars !! 6) == 72 (And this one was clearly a bitwise XOR)

Trying to untangle all of this manually seemed like a huge headache. The best way forward looked like using a script to parse these conditions and feed them to an SMT solver like Z3.

Step 2: Trial and Error with a Python Solver

So, my plan was to use Python with the z3-solver library to find the flag automatically.

Attempt 1: Simple String Replacement My first idea was a bit naive. I tried to just replace the Haskell operators like (*) and (+) and the array indexing chars !! i with their Python versions. As I probably should have expected, this crashed with a SyntaxError. Haskell uses prefix notation (like (*) a b), which isn’t how Python’s infix notation (a * b) works at all.

Attempt 2: A Basic Parser For my second try, I wrote a slightly smarter parser to deal with the prefix style. It worked for simple cases, but it wasn’t powerful enough for some of the more complex lines in the source file, especially the ones where expressions were nested inside each other, like (*) ((*) a b) c. This attempt ended with a ValueError because my simple parser got confused by the extra parentheses.

Step 3: The Final Solution - A Robust Recursive Parser

After those failures, it was clear I needed a more solid parser that could actually understand the nested structure of the Haskell code. The solution that finally worked was a recursive-descent parser.

The idea behind this kind of parser is that it breaks down each line into tokens and then builds a Z3 expression tree by calling itself to handle any nested parts. This approach correctly handled the structure and all the different operators. My final script reads through all 57 conditions, converts each one into a Z3 constraint, and adds it to the solver. I also added one more rule: that all the characters in the flag had to be printable ASCII (with values from 32 to 126).

Here is the Python script that finally cracked it:

# solve.py
import re
import shlex
from z3 import Solver, BitVec, sat

def solve_flag_from_file(filename):
    try:
        with open(filename, 'r') as f:
            content = f.read()
    except FileNotFoundError:
        print(f"❌ Error: Can't find '{filename}'.")
        print("Is 'success.hs' in the same folder?")
        return

    s = Solver()

    c = [BitVec(f'c_{i}', 8) for i in range(39)]

    # This map helps translate the Haskell operators to Z3 functions.
    op_map = {
        "*": lambda a, b: a * b,
        "+": lambda a, b: a + b,
        "-": lambda a, b: a - b,
        ".|.": lambda a, b: a | b,   # This is OR in Haskell
        ".&.": lambda a, b: a & b,   # This is AND
        "xor": lambda a, b: a ^ b    # XOR is the same
    }

    def parse_expression(tokens):
        """
        This is the tricky part. A recursive function to turn a list of
        string tokens into a Z3 expression tree.
        """
        token = tokens.pop(0)

        if token == '(':
            op_str = tokens.pop(0)

            # Sometimes there are nested parens around the operator, gotta handle that.
            if op_str == '(':
                op_str = tokens.pop(0)
                tokens.pop(0) 

            op_func = op_map.get(op_str)
            if not op_func:
                # If we don't know the operator, we have to stop.
                raise ValueError(f"Unknown op: '{op_str}'")

            operands = []
            while tokens and tokens[0] != ')':
                operands.append(parse_expression(tokens))

            if not tokens or tokens.pop(0) != ')':
                raise SyntaxError("Mismatched parens or bad expression.")

            if len(operands) != 2:
                raise SyntaxError(f"Op '{op_str}' needs 2 args, got {len(operands)}.")

            return op_func(operands[0], operands[1])

        elif re.fullmatch(r"c\[\d+\]", token):
            return c[int(token[2:-1])]

        elif re.fullmatch(r"-?\d+", token):
            # Or if it's just a number.
            return int(token)

        else:
            op_func = op_map.get(token)
            if not op_func:
                raise ValueError(f"Bad token or unknown op: '{token}'")
            
            operand1 = parse_expression(tokens)
            operand2 = parse_expression(tokens)
            return op_func(operand1, operand2)

    if_conditions = re.findall(r'if (.*) then do', content)

    print(f"Found {len(if_conditions)} constraints. Starting parse...")

    for i, condition in enumerate(if_conditions):
        try:
            lhs_str, rhs_str = condition.strip().split(' == ')
            rhs_val = int(rhs_str) # The right side is the easy part.


            lhs_str = re.sub(r"\(chars !! (\d+)\)", r"c[\1]", lhs_str)
            

            lhs_tokenizable = f"( {lhs_str} )"
            lhs_spaced = lhs_tokenizable.replace('(', ' ( ').replace(')', ' ) ')
            tokens = shlex.split(lhs_spaced)

            lhs_expr = parse_expression(tokens)
            s.add(lhs_expr == rhs_val)
        except Exception as e:
            print(f"Parse error on condition #{i+1}: {condition}")
            print(f"Detail: {e}")
            return


    for i in range(39):
        s.add(c[i] >= 32, c[i] <= 126) # ASCII 32 (space) to 126 (~)

    print("\nParse complete. Asking Z3 to solve...")
    if s.check() == sat:
        m = s.model()
        result = [chr(m[c[i]].as_long()) for i in range(39)]
        flag = "".join(result)
        print("\n✅ Success! Z3 found the flag:")
        print(flag)
    else:
        # Aww, no solution.
        print("\n❌ Z3 says it's unsolvable. Maybe a bug in my parser?")

if __name__ == "__main__":
    solve_flag_from_file('success.hs')

$ python solve.py
Found 57 constraints. Starting parse...
Parse complete. Asking Z3 to solve...
✅ Success! Z3 found the flag:
.;,;.{imagine_if_i_made_it_compiled!!!}

flag: .;,;.{imagine_if_i_made_it_compiled!!!}